√ 扇形 中心角 求め方 面積 151605

中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット

面積の求め方 扇形 扇形の面積を求める公式は、次の通りです。 S = πr2 × x 360 = 1 2lr S = π r 2 × x 360 = 1 2 l r 中心角 x°、半径 r の扇形 ここで、S は扇形の面積、π は円周率、r は円の半径、x は中心角（単位「度」）を表します。 また、2行目の l は扇形の電卓の使い方 おうぎ形の半径と中心角を入力して「計算」ボタンを押すと、おうぎ形の面積と弧の長さが計算されます。 円周率は変更できます。 円周率で「πを使う」にチェックを入れると円周率をπとして計算します。 半径を求めたい場合は、中心角

扇形 中心角 求め方 面積

扇形 中心角 求め方 面積-円に内接する四角形の面積（4辺から） 四角形の面積（4辺と対角の和から） 正多角形の面積 正多角形の面積から辺 円の面積 円の面積から半径 扇形の面積 弓形の面積（中心角から） 弓形の面積（弓形の半径と高さから） 弓形の面積（弓形の弦長と高さ演習問題で理解を深めよう！ （1）半径 ㎝、面積 cm²のおうぎ形の中心角を求めなさい。 （1）解説＆答えはこちら 答え おうぎ形の面積が与えられているので こちらの公式を利用します。 まずは、半径9㎝の円の面積を求めます。 そして、公式に

扇形の面積の求め方 公式と計算例

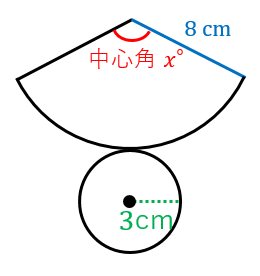
半径3cmで面積が3π㎠のおうぎ形の中心角を求めます。 まずは同じ半径 (3㎝)を持つ円の面積を求めます。 3×3×π＝9π あとは公式に当てはめていくと 式が完成します。 あとは約分してやって、計算あるのみ！ これで中心角が1°だと求めることができ 扇形の中心角の大きさの求め方を教えてください 当てはめのところで、『360分の中心角 ＝ 分の面積』となっているのですが、 の場所に何が入るかわかる方はいませんか？ 扇形の面積の求め方は、半径と中心角から求める方法が一般的です。 半径と中心角から扇形の面積を求める 扇形の面積は、 半径 × 半径 × 円周率 × θ / 360 で求めることができます。 半径rの円の面積の θ / 360 倍の大きさで求める方法です。 頭の中に

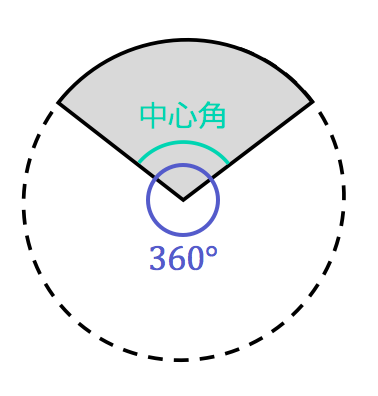
数学・算数 中1 数学 扇形 中1 数学 扇形 半径 3cm 中心角 60° の「扇形の面積と弧の長さ」の求め方を詳しく教えてください。 今までやったのと違うので解けません、助けてください。 質数学Ⅱ（三角関数）：円弧の長さと扇形の面積（弧度法） 対象 高2 再生時間 328 説明文・要約 〔半径 r、中心角 θ（ラジアン）の扇形について〕 ・円弧の長さは rθ 円周の長さ 2πr に対して、中心角の割合が θ/2π であるため もしくはおうぎ形の公式 弧の長さ ＝ 円周 × 中心角 360° 中 心 角 360 ° ＝ 直径×314 × 中心角 360° 中 心 角 360 ° おうぎ形の面積 ＝ 円の面積 × 中心角 360° 中 心 角 360 ° ＝ 半径×半径×314 × 中心角 360° 中 心 角 360 ° 重要なのは、 おうぎ形が元の円と比べた時に

扇形 中心角 求め方 面積のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

1	1	1
1	1	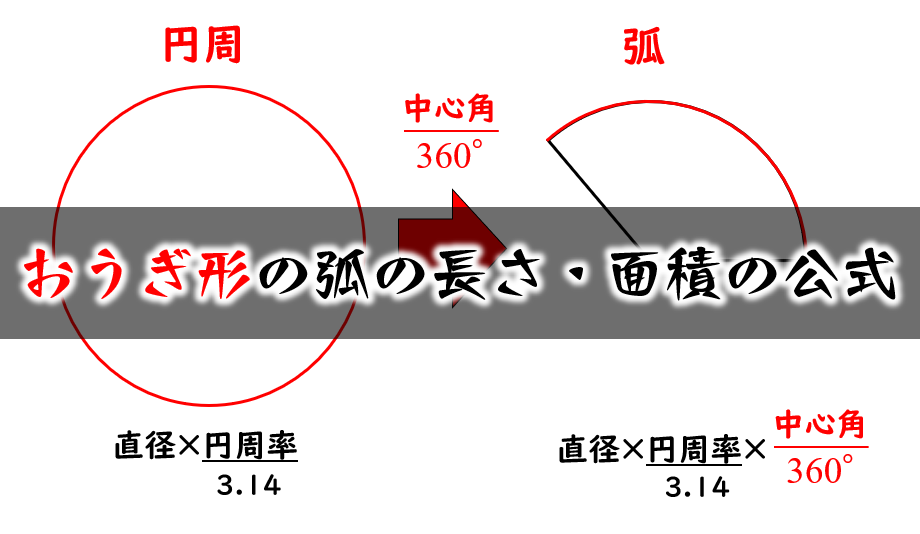1
1	1	1
1	1	1
1	1	1
1	1	1
1	1	1
1	1	1
1	1	1
1	1	1
1	1	1
1	1	1
1	1	1
1	1	1
1	1	1
1	1	1
1	1	1
1	1	1
1	1	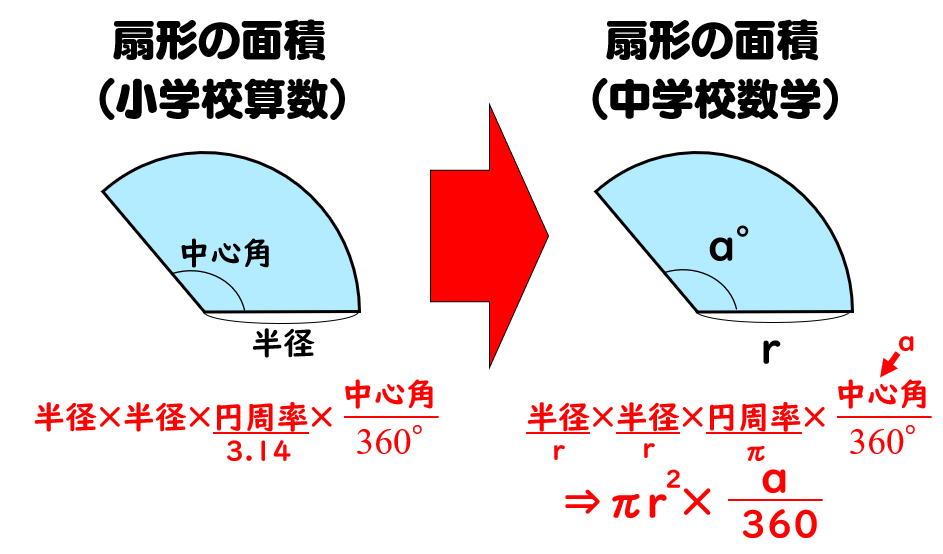1
1	1	1
1	1	1
1	1	1
1	1	1
1	1	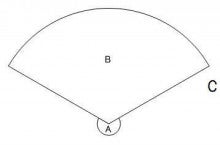1
1	1	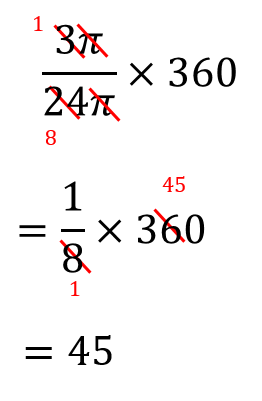1
1	1	1
1	1	1
1	1	1
1	1	1
1	1	1
1	1	1
1	1	1
1	1	1
1	1	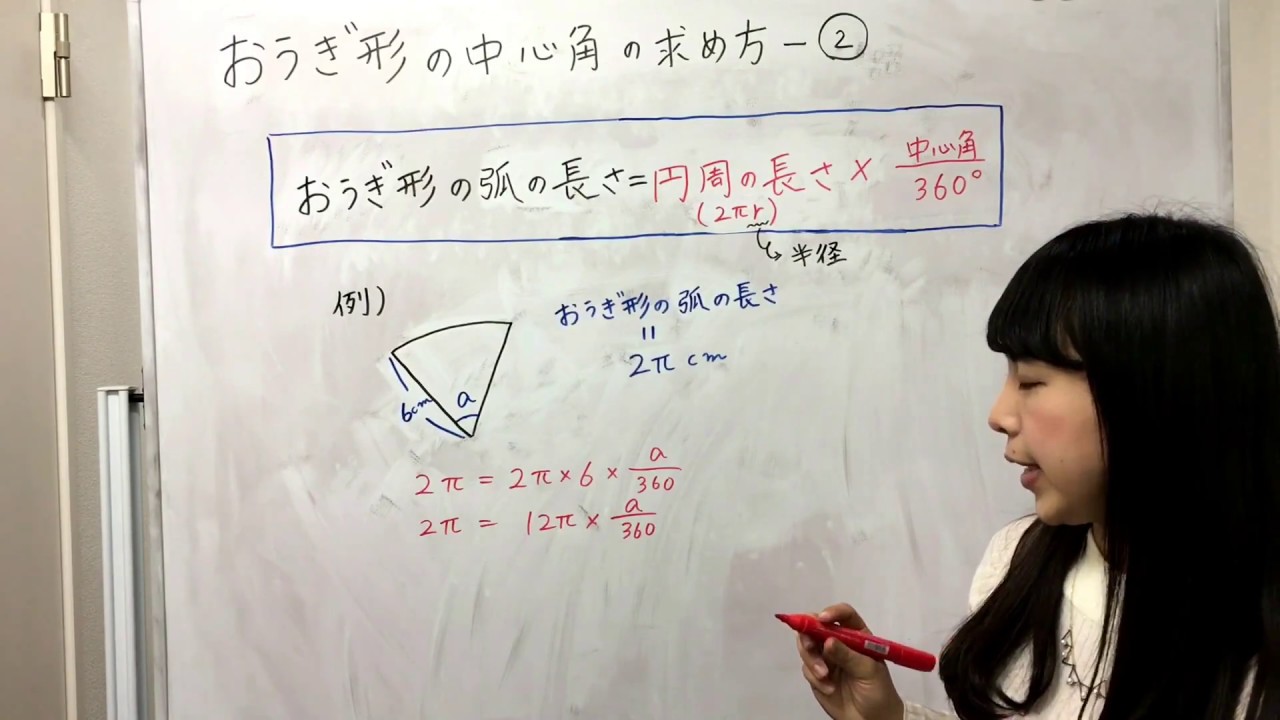1
1	1

 円・扇形の公式まとめ 円周： 2πr 2 π r 円の面積： πr2 π r 2 扇形の弧の長さ： 2πr× a 360 2 π r × a 360 扇形の面積： πr2 × a 360 π r 2 × a 360 扇形の面積（弧の長さ l l からの導出）： 1 2lr 1 2 l r ※半径： r r 、円周率： π π 、中心角： a a 、扇形の弧の長さ 扇形の面積の求め方の公式！ 「 おうぎ形の面積の求め方 」はつぎの公式であらわされるんだ。 半径をr、面積をS、円周率をπ、中心角をαとすると、 S = πr² × α / 360 になるんだ。 つまり、 円周率×半径×半径×中心角÷360 ってわけさ。 たとえば