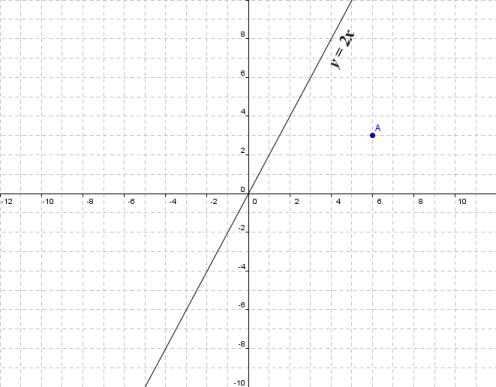
Find the matrix A that induces T if T is reflection over the line y=−3/2x Please give me the solution Using a rule and a pair of compasses only, construct triangle XYZ, such that line XY = 5cm, line XX=4cm and line YZ =6cm The image of a point after a reflection over the line y = –x is (7, –1) Find the coordinates of theXyplane, the x and ycoordinates stay the same, but the zcoordinate becomes zero The formula for the transformation is then T x y z = x y 0 ⇀u x T ⇀u y z Let's now look at the above example in a different way Note that the xyplane is a 2dimensional subspace of R3 that corresponds (exactly!) with R2 We can therefore look at theThe line of reflection is usually given in the form y = m x b y = mx b y=mxby, equals, m, x, plus, b How do I draw the line of reflection?
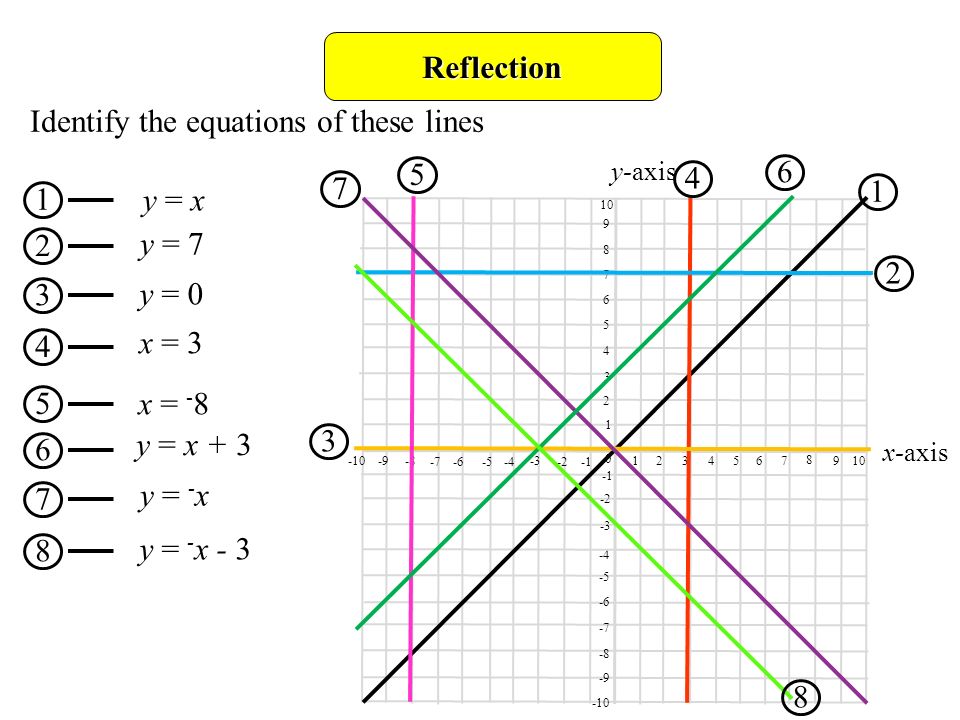
Matrices As Transformations
Reflection over the line y xy x of the point
Reflection over the line y xy x of the point-For a reflection over the x − axis y − axis line y = x Multiply the vertex on the left by 1 0 0 − 1 − 1 0 0 1 0 1 1 0Reflection in a Line A reflection over a line k (notation r k) is a transformation in which each point of the original figure (preimage) has an image that is the same distance from the line of reflection as the original point but is on the opposite side of the line Remember that a reflection is a flip Under a reflection, the figure does not change size



2
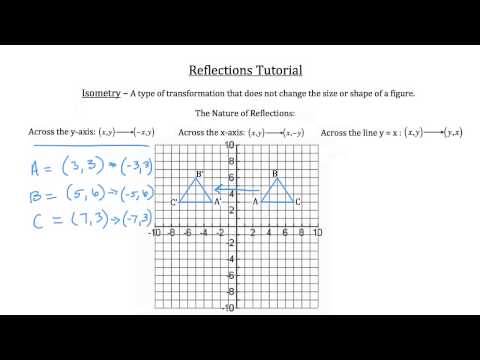
Answer from gabriel SHOW ANSWER After the reflection over the line y = x, the image of the point is (3,2) Stepbystep explanation When a given point is reflected over a line the point only changes place but the distance between the point and the line remains same Let (x,y) be a point on the plane andWhen the line of reflection is the line x = y, as in Figure 5, the equations for the reflection will be x = y', and y = x' These can be used the same way as before The image of (3,1) is (1,3), and the image of the ellipse x 2 4y 2 = 10 is 4x 2 y 2 = 10 (after dropping the Figure 4 Illustration by Hans &Ry−axis(x,y)→(−x,y) Notice that the notation tells you exactly how each (x,y) point changes as a result of the transformation Example A Find the image of the point (3, 2) that has undergone a reflection across a) the xaxis, b) the yaxis, c) the line y=x, and d) the line y=−x Write the notation to describe the reflection Solution 39
How do you find the image of a point in the XY plane?, So, it is clear that the image of point (5,2, 7) with respect to XY–plane is (5,2,7) Now we should find the image of point (4,0,7) with respect to line y=0 Now we should compare y=0 with axbycz=d Furthermore, Where is the image of a point that is on the line of reflection?, A reflection over line is a transformation in3 units up So the reflected point needs to be 3 units above the mirror line The ycoordinate of the mirror line is 2 so 3 up from that is 5Let T R 2 →R 2, be the matrix operator for reflection across the line L y = x a Find the standard matrix T by finding T(e1) and T(e2) b Find a nonzero vector x such that T(x) = x c Find a vector in the domain of T for which T(x,y) = (3,5) Homework Equations The Attempt at a Solution a I found T = 0 11 0
Use our online point reflection calculator to know the point reflection for the given coordinates This calculator helps you to find the point reflection A, for the given coordinates of A (x,y) Just select an axis from the dropdown and enter the coordinates, the point reflection calculator will show the result Point reflection, also called as an inversion in a point is defined as an isometryA ray of light is send along the line x 2y 8 = 0 After refracting across the line x y 1 = 0 it enters the opposite side after turning by 1 5 o away from the line x y 1 = 0, then the equation of the line along which the reflacted ray travel isThe image of the point (4,3) under a reflection across the line y =− x is (− 3, − 4) o True o False Justify your answer The image of the point (− 1, − 5) under a reflection across the y = x is (− 7, − 3) o True o False Justify your answer Point A (1,3) is reflected across the xaxis to create point A ' The line y = 2 x − 5




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com



Reflection Of A Point In Y Axis Reflection Of A Point Reflection
👉 Learn how to reflect points and a figure over a line of symmetry Sometimes the line of symmetry will be a random line or it can be represented by the xWhat is #A'#, the image of #A(3,5)#, after a reflection in the line #y = x#?Q Given triangle JBN with coordinates J (4,5), B (1, 7), and N (7,8), find the image of point B after a reflection over the line y = x Q After a reflection over the xaxis, (5,10) is the image of point N




Chapter 9 Flashcards Quizlet
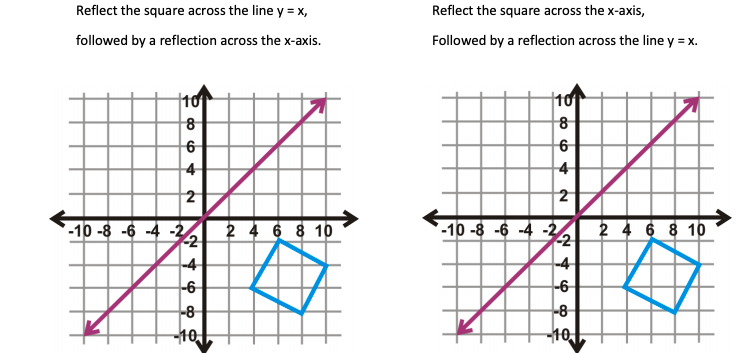



Solved Reflect The Square Across The Line Y X Followed By Chegg Com
Precalculus 1 Answer Jim G image A' = (5 , 3 ) Explanation Any point (x , y ) when reflected in the line y = x has an image ( y , x ) example A (3 , 4 ) has image A' ( 4 , 3 ) Answer link Related questionsWhat is the image of (9, 5) after a reflection over the line y = x?Reflection over the line $$ y = x $$ A reflection in the line y = x can be seen in the picture below in which A is reflected to its image A' The general rule for a reflection in the $$ y = x $$ $ (A,B) \rightarrow (\red B, \red A ) $ Diagram 6 Applet You can drag the point anywhere you want



Matrices As Transformations




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com
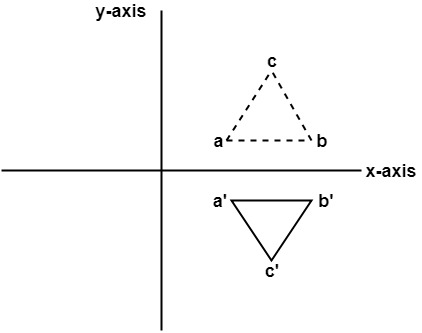
Line segments I end this segment i n over here and T oh this is T oh here are reflected over the line y is equal to negative X minus 2 so this is the line that they're reflected about this dashed purple line and it is indeed y equals negative X minus 2 this right over here is in slopeintercept form the slope should be negative 1 and we see that the slope of this purple line is indeed negative 1 if X changes by a certain amount and Y changes by the negative of that if X changes by 1 YSee Answer Check out a sample Q&A here Want to see this answer and more?Check all that apply The line of reflection, EH, is the perpendicular bisector of BB', AA', and CC' Nice work!
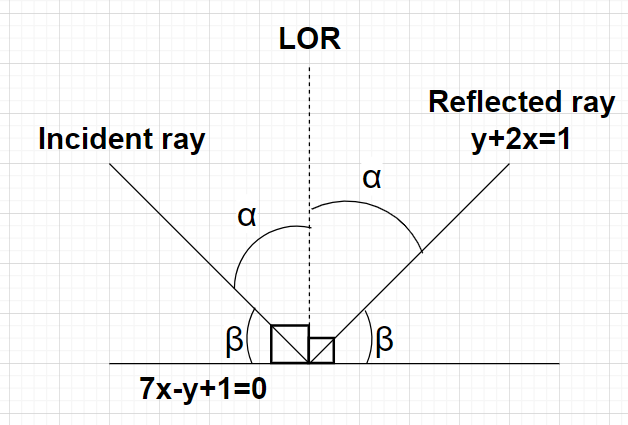



A Ray Of Light Is Incident Along A Line Which Meet Class 11 Maths Cbse




Matrices As Transformations
Answer Let's do it!Reflections What are the coordinates of the image of vertex G after a reflection across the line y=x?If the green line y=x were a mirror, the reflection of the point (8,3) would reflect like the dotted line shows That point is the INVERSE point (3,8) Notice that any time you reflect a point into the line y=x, you get the point with the x and y coordinates switched, called the INVERSE point You should find that interesting!




Reflecting Figures In Coordinate Space Krista King Math Online Math Tutor
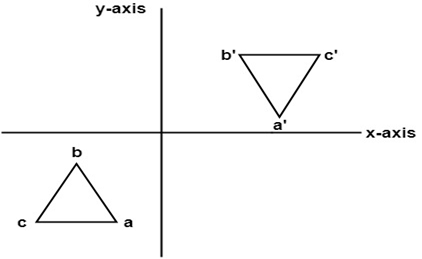



Computer Graphics Reflection Javatpoint
If (a, b) is reflected on the line y = x, its image is the point (b, a) If (a, b) is reflected on the line y = x, its image is the point (b, a) Geometry Reflection A reflection is an isometry, which means the original and image are congruent, that can be described as a "flip"The problem is asking us to reflect the point (8, 7) over the reflection line y = x We will follow the method described in the below videoThe reflection of any point (x, y) in the line y = x is given by (y, x) or the x and ycoordinate will be exchanged to each other Hence reflection of point ( 6 , 8 ) in the line x = y is ( 8 , 6 )




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines
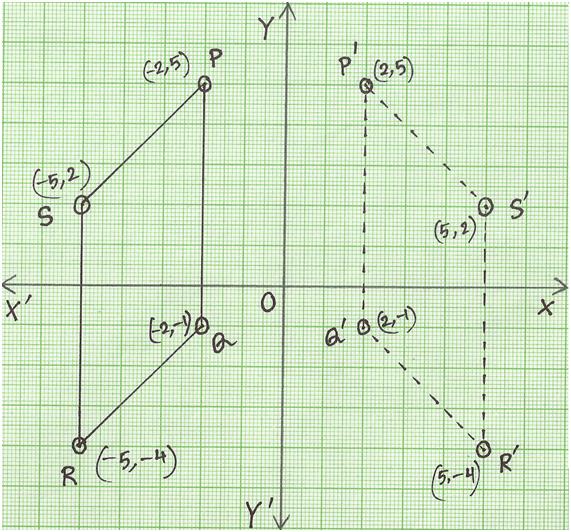
When reflecting coordinate points of the preimage over the line, the following notation can be used to determine the coordinate points of the image r y=x =(y,x) For example For triangle ABC with coordinate points A(3,3), B(2,1), and C(6,2), apply a reflection over the line y=x By following the notation, we would swap the xvalue and the yvalueStack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeThe rule for a reflection over the y axis is ( x , y ) → ( − x , y ) Reflection in the line y = x A reflection of a point over the line y = x is shown



2




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines
Get the free Reflection Calculator MyALevelMathsTutor widget for your website, blog, Wordpress, Blogger, or iGoogle Find more Education widgets in WolframAlphaWhen we're reflect over the line y = x, we switch the x and y coordinates and we make each the opposite, positive or negative sign And in all these cases, the mirror line is always the perpendicular bisector of the segment between the original point and its reflected image, that's an important geometry factWhen reflecting a figure in a line or in a point, the image is congruent to the preimage A reflection maps every point of a figure to an image across a fixed line The fixed line is called the line of reflection A reflection of a point over the line y = − x y = −x is shown The rule for a reflection in the origin is (x, y) → (− y, − x)




Reflection Over The Line Y X Youtube




Reflection Over A Line Expii
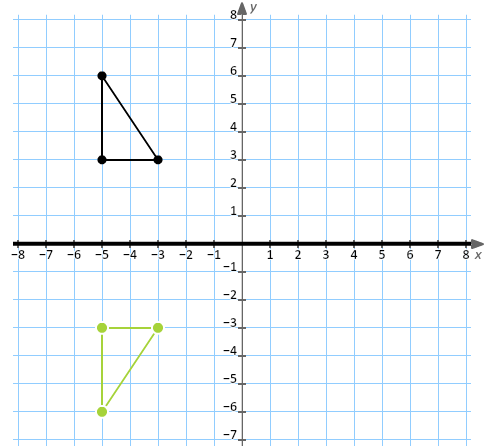
Vertical Reflection Apply a reflection over the line y=1 The procedure to determine the coordinate points of the image are the same as that of the previous example with minor differences that the change will be applied to the yvalue and the xvalue stays the same In the end, we would have A'(6,2), B'(5,7), and C'(5, 3)Yes, the answer is A x=0 Another way to say reflect across the yaxis is to say reflect across the line x=0 since the line created by graphing x=0 is the same as the yaxis An image that is a reflection across the yaxis, or across the line x=0, will have opposite xcoordinates from the preimage but identical ycoordinatesThe point (3,1) will reflect from below the xaxis over the mirror line and end up, above it, keeping the xcoordinate of 3 The ycoordinate needs some working out , how far is it from the mirror line?




Common Reflections Key Stage 3



Math Alive Geometry 1
Email Linear transformation examples Linear transformation examples Scaling and reflections This is the currently selected item Linear transformation examples Rotations in R2 Rotation in R3 around the xaxis Unit vectors Introduction to projections Expressing a projection on to a line as a matrix vector prodReflections flip a preimage over a line to create the image In this lesson we'll look at how the reflection of a figure in a coordinate plane determines where it's located A reflection is a type of transformation that flips a figure over a line The line is called the line of reflection, or the mirror line3) reflection over the xaxis 4) reflection over the yaxis 22 In the diagram below, line m is parallel to line n Figure 2 is the image of Figure 1 after a reflection over line m Figure 3 is the image of Figure 2 after a reflection over line n Which single transformation would carry Figure 1 onto Figure 3?
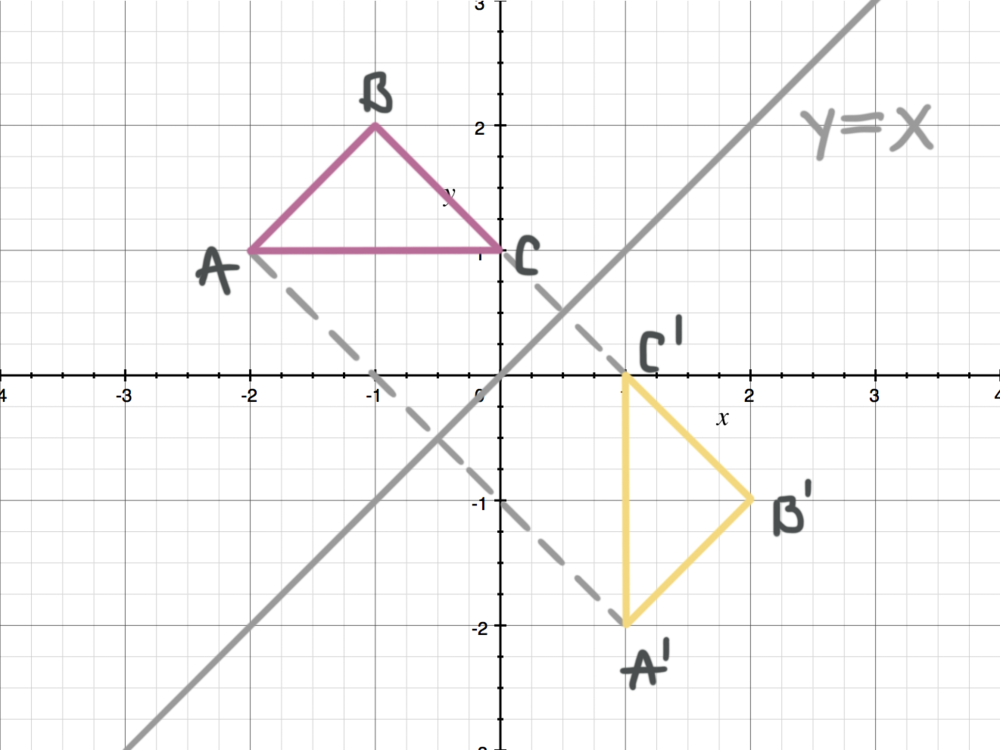



Reflecting Figures In Coordinate Space Krista King Math Online Math Tutor




Reflection Mathbitsnotebook A1 Ccss Math
1) a dilation 2) a rotation 3) aWhat is the image of (−7,5) after a reflection over the line y=−x?The angle measures were multiplied by X Y A B



Reflection Over The X And Y Axis The Complete Guide Mashup Math



What Is The Reflection Over The Y Axis Of The Point 4 7 Quora
Posted on by adminA reflection of a point, a line, or a figure in the X axis involved reflecting the image over the x axis to create a mirror image In this case, the x axis would be called the axis of reflection Math Definition Reflection Over the Y AxisThe linear transformation rule (p, s) → (r, s) for reflecting a figure over the oblique line y = mx b where r and s are functions of p, q, b, and θ = Tan 1 (m) is shown below Finding the linear transformation rule given the equation of the line of reflection equation y = mx b involves using a calculator to find angle θ = Tan 1 (m




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com




Reflecting A Shape In Y X Using Cartesian Coordinates Key Stage 3
Check_circle Expert Answer Want to see the stepbystep answer?Cassidy Courtesy of Gale Group_ Preview this quiz on Quizizz Point 𝐹′ is the image when point 𝐹 is reflected over the line 𝑥 = −2 and then over the line 𝑦 = 3 The location of 𝐹′ is (3, 7) Which of the following is the location of point 𝐹?




Transformations On The Coordinate Plane



Reflection Transformation Solutions Examples Videos
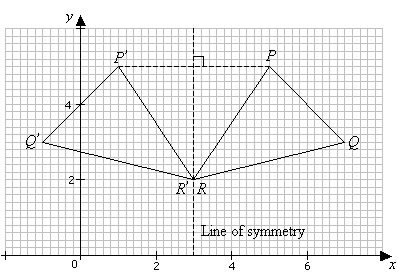
Each point in the starting figure is the same perpendicular distance from the line of reflection as its corresponding point in the imageQ The reflection of K (2,8) is K' (8, 2) What is the line of reflection?A'B'C' was constructed using ABC and line segment EH For transformation to be reflection, which statements must be true?



Computer Graphics Reflection Javatpoint
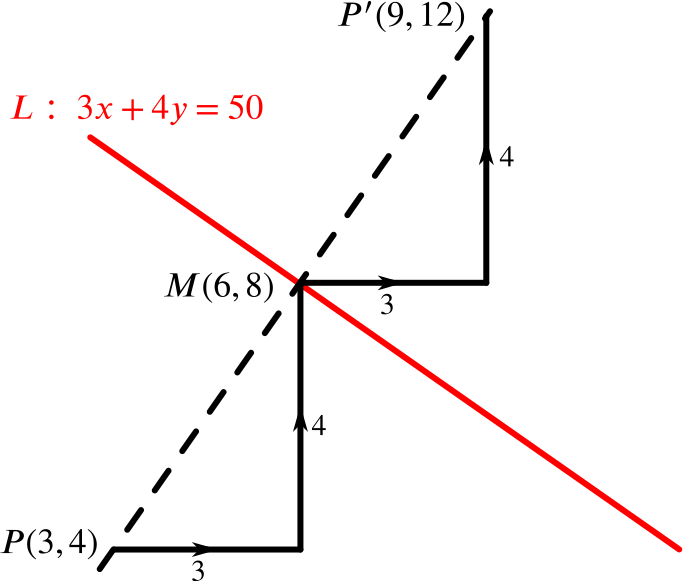



Solution Can We Reflect This Point In This Line Geometry Of Equations Underground Mathematics
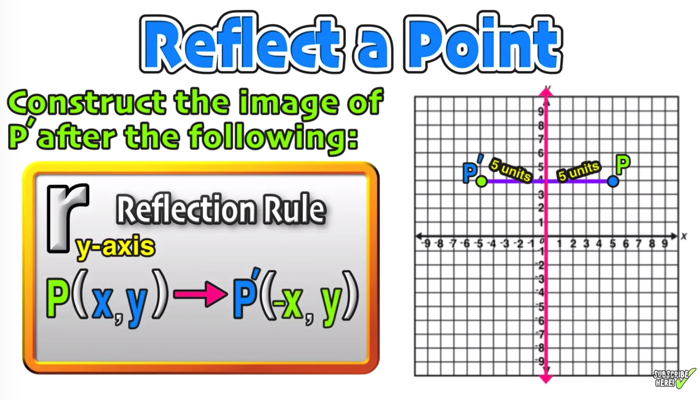
(4,1) after reflection over the yaxis would become color(red)((4,1)) A reflection over the yaxis leaves the point the same distance above the xaxis (that is the ycoordinate value does not change) The xcoordinate value becomes an equal distance from the yaxis but on the other side of the yaxis (that is the xcoordinate value becomes the negative ofAnd also, the line x = 2 (line of reflection) is the perpendicular bisector of the segment joining any point to its image Students can keep this idea in mind when they are working with lines of reflections which are neither the xaxis nor the yaxisWhat is the image of (0,8) (0,−8) after a reflection over the line y=xy=x?




Reflections Through The Axes And The Lines Y X And Y X Geogebra



How To Prove Say That Point X Y Becomes Y X On A Reflection On The Line Y X Using Only Geometry Quora
The rule for reflection over the yaxis is (x, y) >What the image of ( 6, 5) after a reflection over the line y = x ?Categories Uncategorized Leave a Next Post Next Sketch the region in the xyplane defined by the inequalities x − 3y2 ≥ 0, 2 − x − 5y Recent Posts What is the equation of a line perpendicular to y=1/4x2 that passes through the point (0,1) First, assume that



Reflecting Points Video Reflections Khan Academy




Reflecting A Shape In Y X Using Cartesian Coordinates Key Stage 3
This video demonstrates how to reflect a figure over the line y=x It shows two methods of reflecting over y=x The video shows how to count towards the y=xA reflection of the point across the line y = x a reflection of the point across the line y = x y − 1 = 2(x − 4) y − 1 = −2(x − 4) In the diagram, DC is 10 units and BC is 6 units ΔRST can be mapped to ΔACB by a reflection over the xaxis and a translation 2 units to the leftThe Lesson A shape can be reflected in the line y = −x If point on a shape is reflected in the line y = −x both coordinates change sign (the coordinate becomes negative if it is positive and vice versa) the xcoordinate becomes the ycoordinate and the ycoordinate becomes the xcoordinate The image below shows a point on a shape being reflected in the line y = −x



Reflection Objectives D Gradereflect Shapes In Lines Such As X 2 Or Y 1 Describe Reflections Fully Identify Reflection Symmetry In 3 D Solids Prior Ppt Download




Reflecting A Shape In Y X Using Cartesian Coordinates Key Stage 3
Given function xy5=0 Find rotation of axes to eliminate xy term




Reflections Across Y X Geogebra




Reflection In The Line Y X Transformation Matrix Youtube



What Is The Image Of 8 7 8 7 After A Reflection Over The Line Y Xy X Quora



Computer Graphics Reflection Javatpoint



Reflection In A Cartesian Plane Lexique De Mathematique




A Line Segment Goes From 1 2 To 4 1 The Line Segment Is Reflected Across X 1 Reflected Across Y 3 And Then Dilated About 2 2 By A Factor
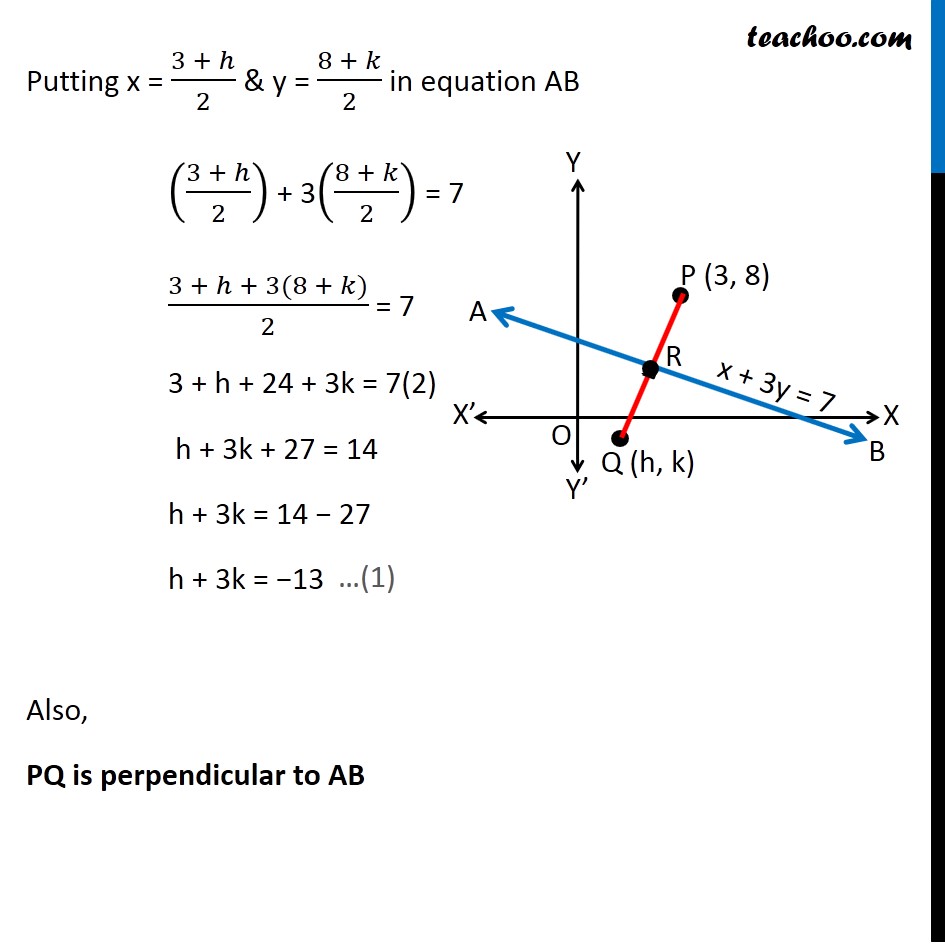



Misc 18 Find Image Of 3 8 With Respect To Line X 3y 7



1




Learn About Reflection Over The Line Y X Caddell Prep Online




Reflection Mathbitsnotebook A1 Ccss Math



2
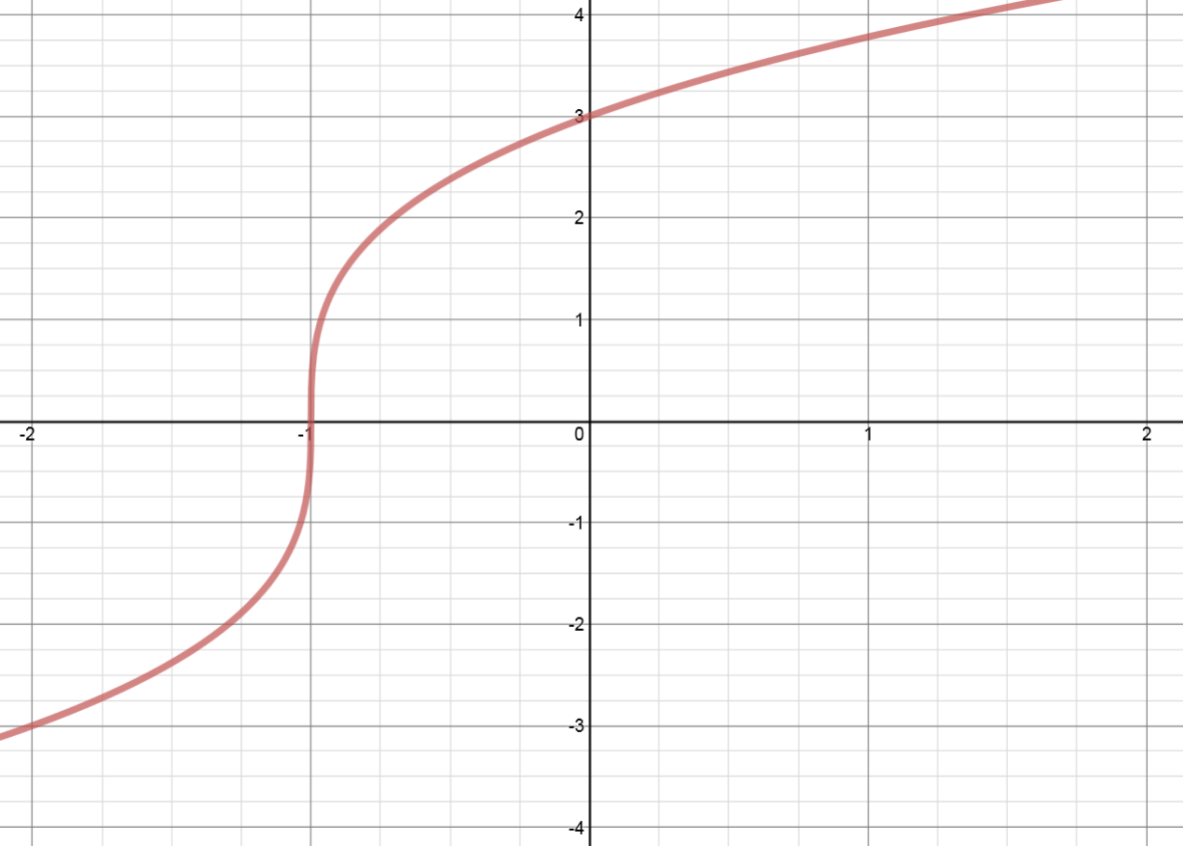



How To Reflect A Graph Through The Y Axis Studypug
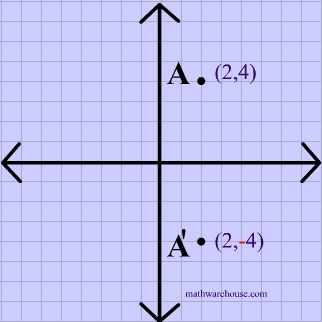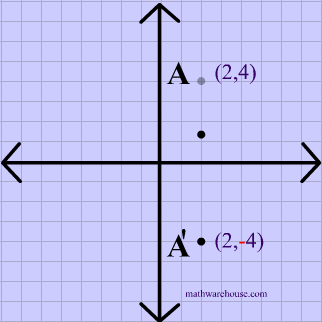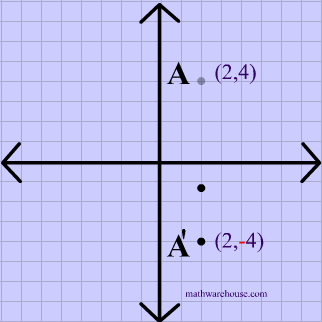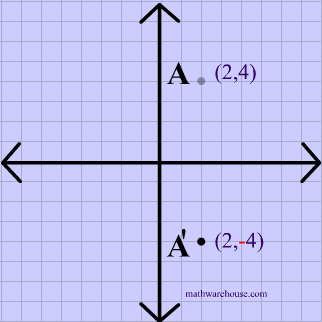



Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines



1




How To Reflect A Graph Through The X Axis Y Axis Or Origin Interactive Mathematics




Reflection Over The Line Y X Math Showme




Reflections
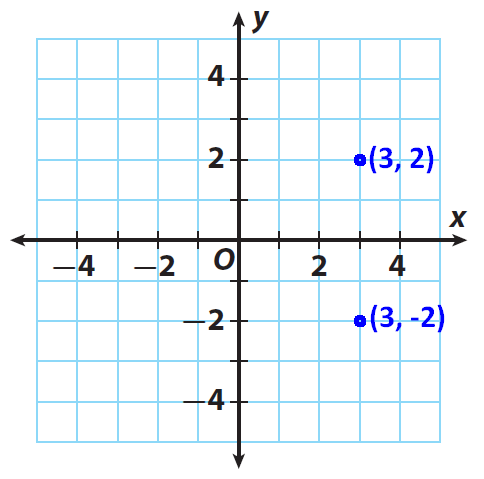



Reflecting In The Coordinate Plane




10 Math Problems Transformation Reflection




Algebraic Representations Of Reflections



3
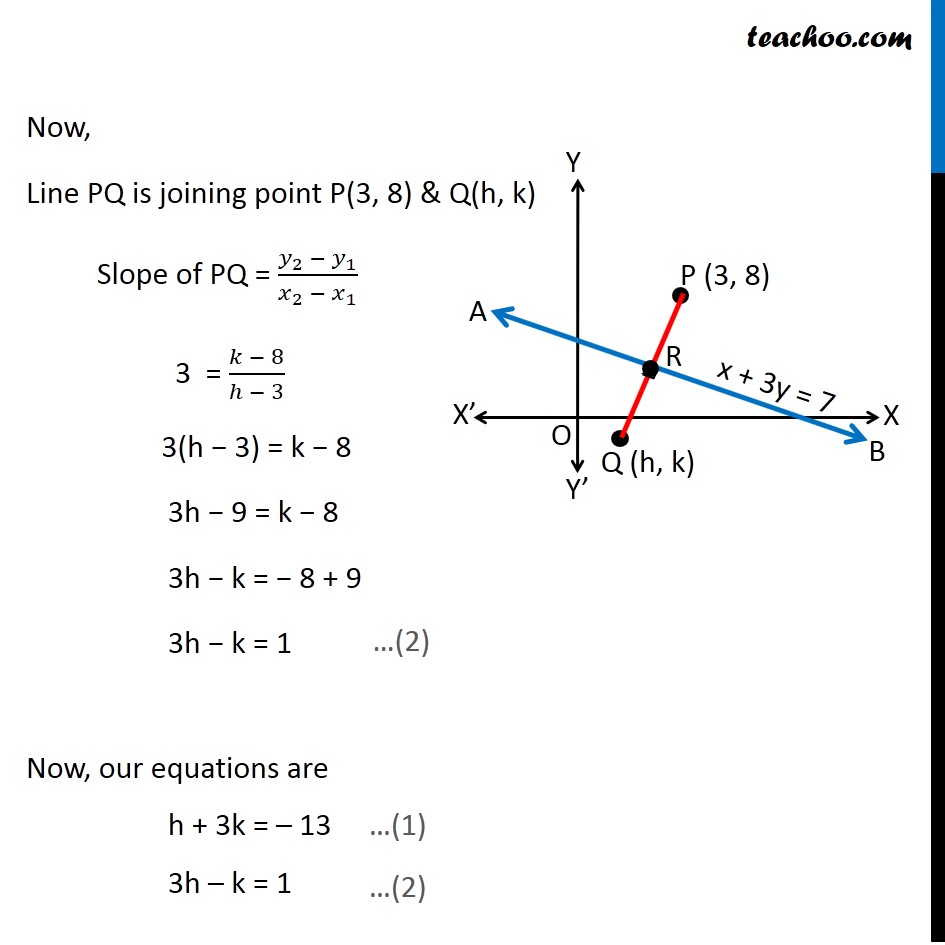



Misc 18 Find Image Of 3 8 With Respect To Line X 3y 7
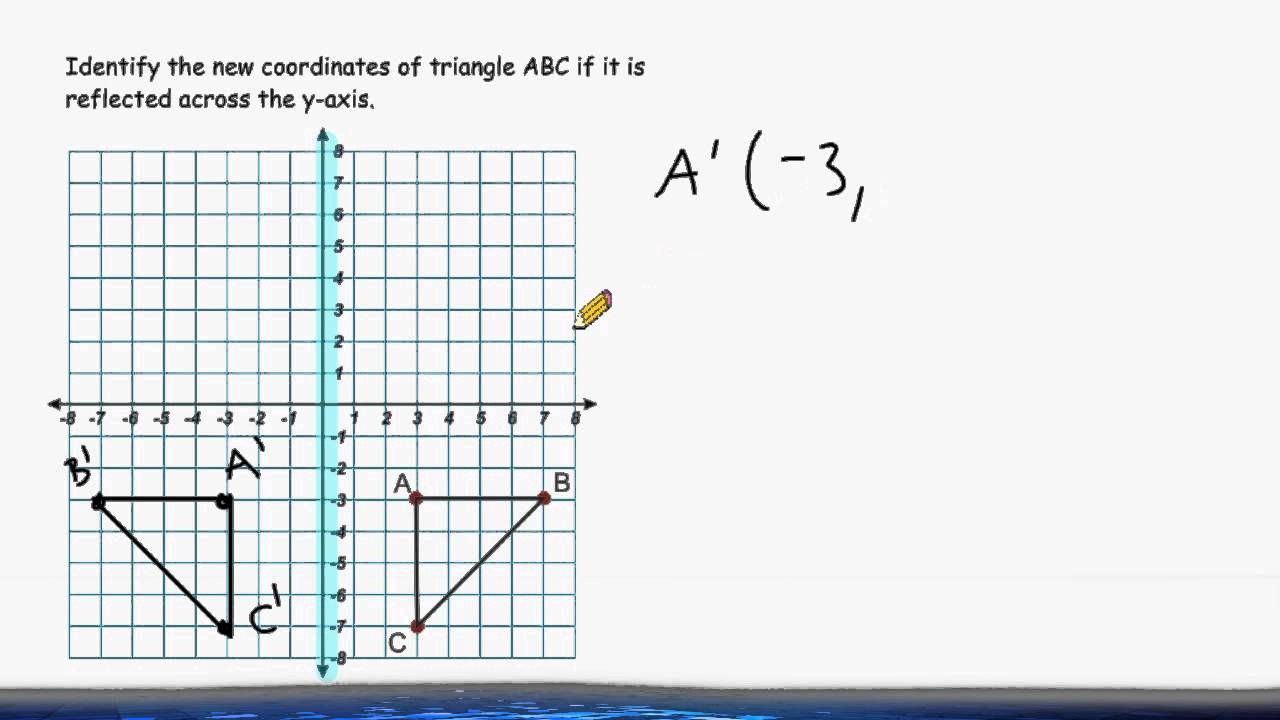



Reflecting A Triangle Across The Y Axis




How To Find A Reflection Image
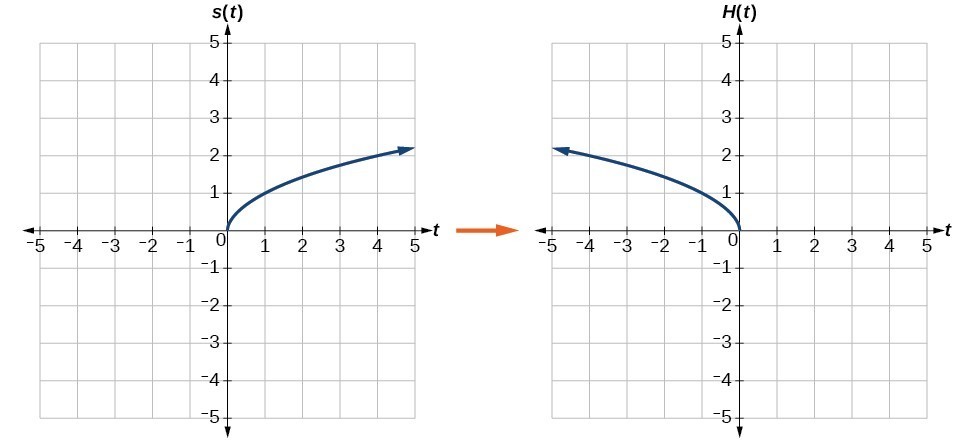



Graph Functions Using Reflections About The X Axis And The Y Axis College Algebra
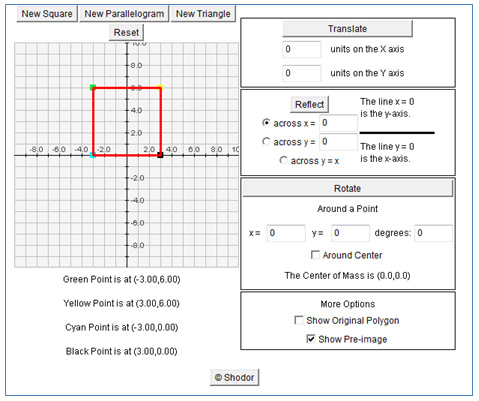



Graphing Dilations Reflections And Translations Texas Gateway
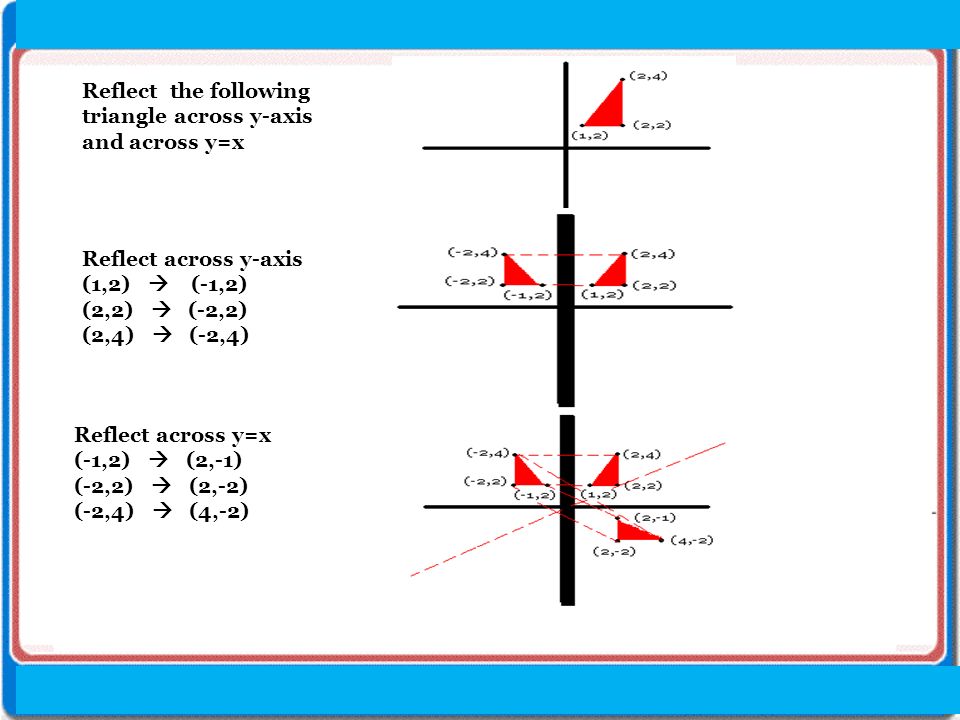



Reflections 30 Reflect Across Y X X Y Y X Reflect Across X Axis X Y X Y Reflect Across Y Axis X Y X Y Reflect Across Y X Reflect Across Ppt Download




Reflecting Shapes Article Reflections Khan Academy
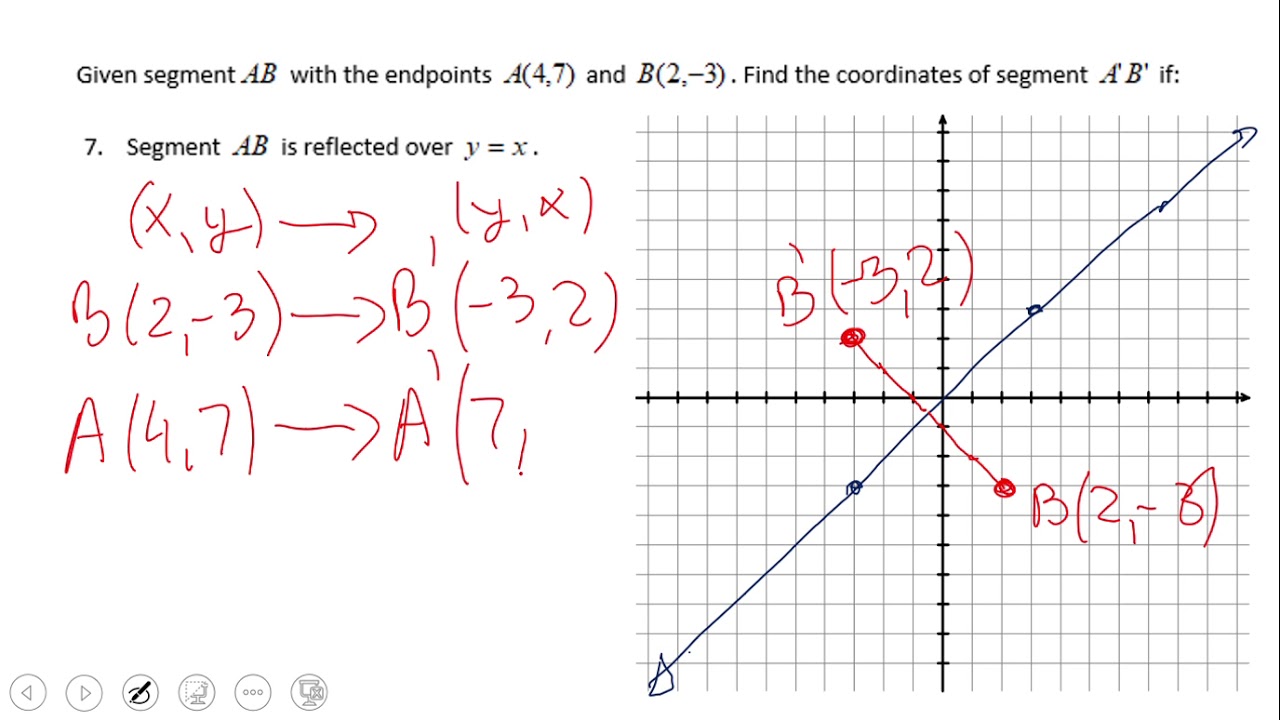



Reflection Over Y X And Y X Youtube



Point 4 3 Is Reflected Over The Line Y X What Are The Coordinates Of The Reflection Mathskey Com



Transformation Matrices Reflection The Line Y X Examsolutions Maths Tutorials Youtube




Reflection Rules How To W 25 Step By Step Examples




Reflection Over The Line Y X Geogebra




Reflection Mathbitsnotebook A1 Ccss Math



Operations On Functions Reflections And Rotations Sparknotes




How To Find Coordinates Of Reflected Point Mathematics Stack Exchange




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com



What Is The Image Of 2 5 Reflected Across X 2 Socratic
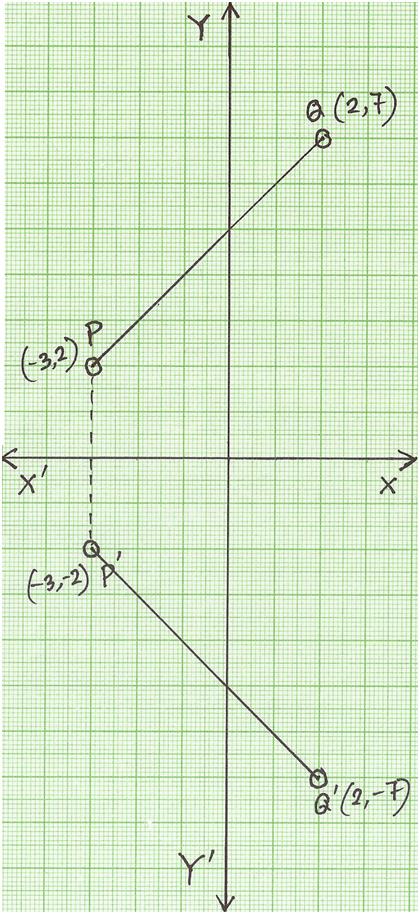



Reflection Of A Point In X Axis Reflection Of A Point Reflection



1
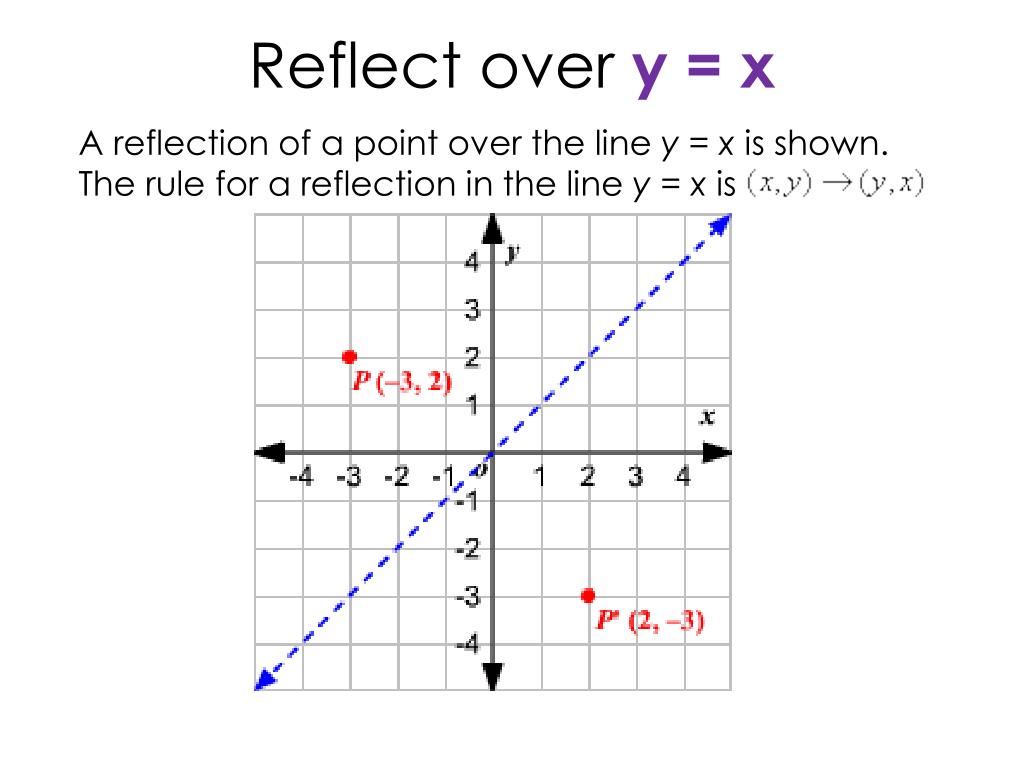



Ppt Reflect Over Y X Powerpoint Presentation Free Download Id
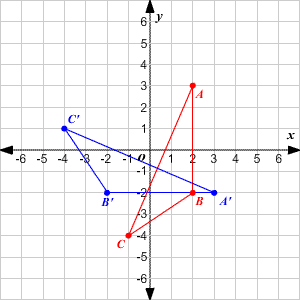



Transformations Of Graphs




Reflection Over Y X Math Geometry Showme



Reflections Of A Graph Topics In Precalculus



Reflection Of A Point In X Axis Reflection Of A Point Reflection




Reflection Mathbitsnotebook A1 Ccss Math



Reflection Over The X And Y Axis The Complete Guide Mashup Math



Reflect Function About Y Axis F X Expii



Reflect Points Over The X And Y Axes Learnzillion




Reflection Mathbitsnotebook A1 Ccss Math
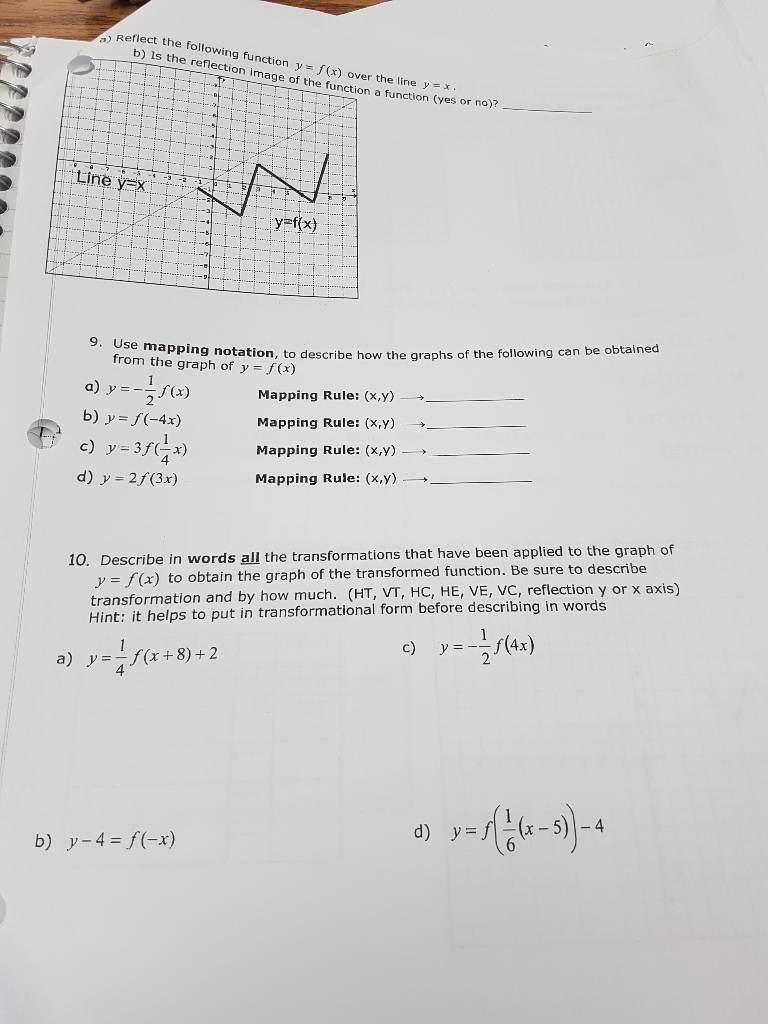



Solved Reflect The Following Function Y F X Over The Line Chegg Com




D Reflection Across Y X Brainly Com
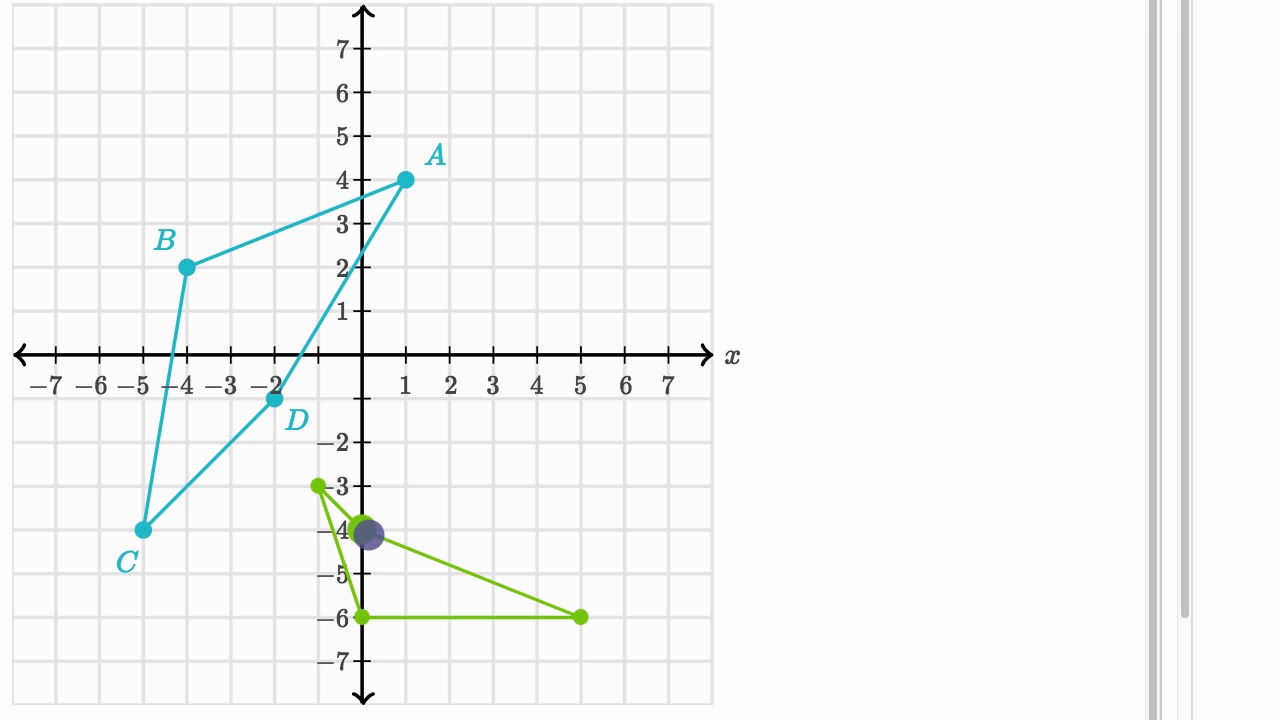



Reflecting Shapes Video Reflections Khan Academy




Reflection In The Line Y X Geogebra



Translations And Reflections Activity Builder By Desmos




Reflect Function About Y Axis F X Expii




Reflection Transformation Solutions Examples Videos




What Are The Coordinates Of Point A 4 1 After It Has Been Reflected Over The Y Axis Socratic




Reflection Over The Y X Line Youtube




Transformation Reflection Over The Line Y X Youtube



2




If Triangle Xyz Is Reflected Across The Line Y 1 To Create Triangle X Y Z What Is The Ordered Brainly Com




10 Math Problems Transformation Reflection



Biomath Transformation Of Graphs
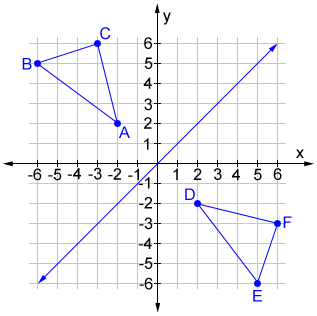



Reflection



What Does It Mean To Reflect Over The Y X Line Quora




Reflection Rules How To W 25 Step By Step Examples



2



2



Reflection Notes Videos Qa And Tests Grade 9 Optional Mathematics Transformation Kullabs


